
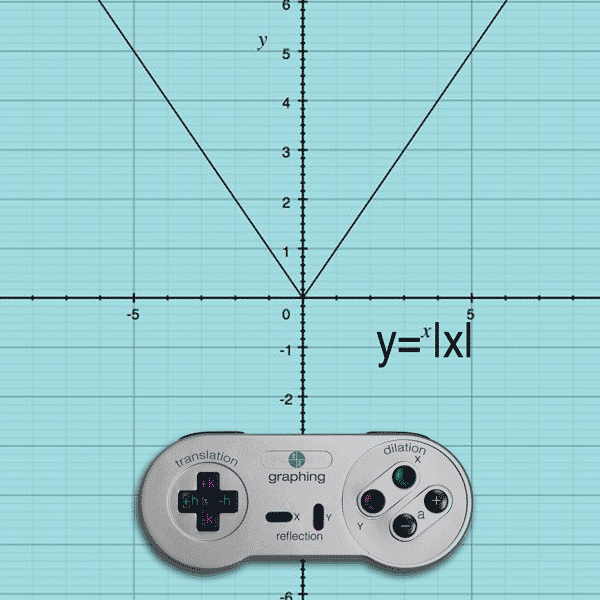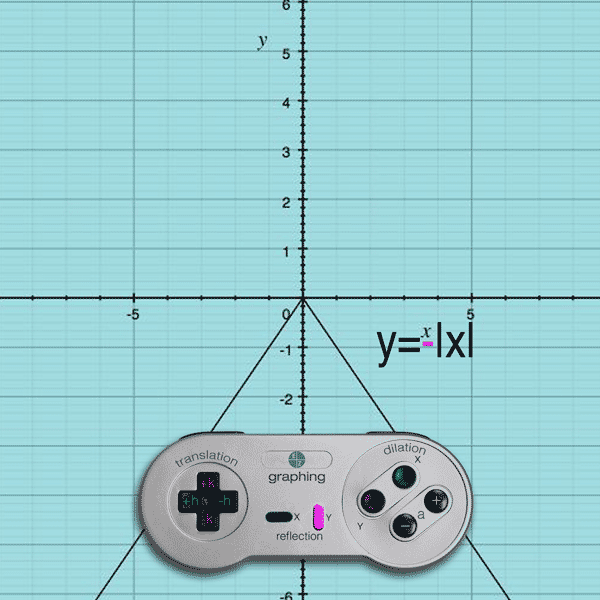
To see how to graph the function using transformations, long division or synthetic division on the original function must be done to obtain a more user friendly form of the equation. In the second picture, the image is first reflected over y axis, then it is translated 1 unit down. In the first picture, though the image is reflected, but it is reflected over y axis. Only the sign of y-coordinate is changed, keeping x-coordinate intact. Hence, the function that represents the reflection of f(x) over the x-axis is. While reflecting a point over x axis, (x, y) (x, -y) rule is followed. See x-coordinates Absolute value function, properties of, 556.

So, Now putting the value of in above expression, we get. When we reflect across the y-axis, the image point is the same height, but has the opposite position from left to right. The 5 inside the parentheses represents a shift right 5 units, and the 7 on the outside represents a shift down 7 units. Reflections create mirror images of points, keeping the same distance from the line. You will show where A (x,y) would be reflected over the x-axis and y-axis. Now, the rule of reflection over the x-axis is (x,y) becomes (x,-y). We can plot points after reflecting them across a line, like the x-axis or y-axis. absolute value between the numbers shown on the ruler. When a rational function consists of a linear numerator and linear denominator, it is actually just a translation of the reciprocal function. The function that represents the reflection of f(x) over the x-axis is. Consider the basic graph of the function: y f(x) All of the translations can be expressed in the form: y a f b (x. To reflect about the x-axis, multiply f(x) by -1 to get -f(x).

To reflect about the y-axis, multiply every x by -1 to get -x. \(\qquad\qquad\)shift left \(2\) units, reflect over the \(x\)-axis, A function can be reflected about an axis by multiplying by negative one.


 0 kommentar(er)
0 kommentar(er)
